Join the new world

Para ciertas situaciones tales como una partícula que no está confinada en un pozo potencial y que se está desplazando libremente de un lado a otro, necesitamos algo que nos permita describir al menos la posición de esa partícula libre, algo que nos permita situarla como una partícula puntual en cierto sistema de coordenadas como (x,y,z). Para hacer frente a esta necesidad, el físico-matemático inglés Paul Adrien Maurice Dirac propuso un nuevo tipo de función conocida en nuestros días como la función delta de Dirac. Esta función, extremadamente impropia (matemáticamente hablando, es casi una imposibilidad, que sin embargo puede ser manipulada matemáticamente), está inspirada directamente en el delta de Kronecker, definido de la manera usual:

δij = 1 para i = j

δij = 0 para i ≠ j

en donde i y j son números discretos (enteros). Lo que se quiere es tomar el concepto del delta de Kronecker haciéndolo extensivo para sub-índices que representan cantidades continuas que en principio pueden tomar cualquier valor que forme parte del conjunto de los números reales. Con esto en mente, definiremos a la función delta de Dirac como una función límite. Considérese la siguiente figura:

El área de esta figura, colocada de modo tal que está centrada en la coordenada x.=.x’, es obviamente igual a la unidad, o sea que A = (a)(1/a) = 1.

A continuación, iremos recortando el ancho de la figura y ampliando al mismo tiempo su altura, de modo tal que el área siga siendo la misma, igual a la unida😛

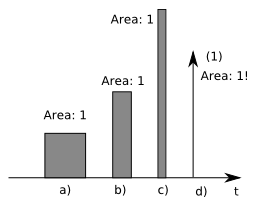
Obsérvese que en (d) hemos llevado al extremo el proceso iniciado en (a) y continuado en (b) y en (c). En efecto, le hemos dado a la figura una altura infinitamente grande, y una anchura infinitamente pequeña. Esto de primera vista puede parecer absurdo, pero si lo consideramos como un proceso límite, no hay nada errado en lo que hemos hecho. Hemos mantenido todo el tiempo el “área bajo la curva” igual a la unidad.

En base al proceso extremo que hemos llevado a cabo, se antoja tentador definir a esta función de la manera siguiente situando el “pico” en una posición x.=.a en donde a puede ser igual a cero (situando el “pico” en el centro del sistema de coordenadas) :

La desventaja de esta definición por sí sola es que involucra un infinito que no se presta a la manipulación matemática. Tenemos que ampliarla (o confinarla) de alguna manera.

Una forma de ampliar la definición de nuestra función extrema sería basarnos en el hecho de que el “área bajo la curva” es igual a la unidad, y en el cálculo infinitesimal ya hay una forma de definir el “área bajo la curva” para cualquier función dentro de un rango a.≤.x.≤.b para la variable independiente:

Esta definición del “área bajo la curva” es una definición precisa, exacta, que se presta a la manipulación matemática; es el resultado de ir subdividiendo el área bajo la curva que hay debajo de una función cualesquiera:
y sumar el área de los rectángulos entre x1.=.a y x2.=.b para obtener de este modo una buena aproximación al área. A cada uno de estos rectángulos le damos la misma anchura Δx, y cada rectángulo tendrá una altura diferente en cada punto xn de la función. Esta manera de definir a la integral es conocida más formalmente como una integración mediante sumas de Riemann, y la noción intuitiva de llevar a cabo una sub-división del área bajo la curva en rectángulos cada vez más pequeños para aproximar el área real es conocida como la regla del rectángulo. En el proceso extremo, llevamos a cabo la subdivisión hasta el infinito, haciendo la anchura de cada rectángulo lo más cercano a cero que podamos (Δx→0) y sumando las contribuciones de una cantidad prácticamente infinita de rectángulos, lo cual en el proceso límite de la definición de la integral puede ser simbolizado de la siguiente manera:


con lo cual queda definida el área bajo la curva como el resultado de un proceso de integración o suma de áreas infinitesimales:

Puesto que en el proceso de construcción de nuestra función extrema se utilizó precisamente el área bajo la curva manteniéndose todo el tiempo igual a la unidad, y puesto que a los rectángulos, o mejor dicho, al rectángulo límite, se le fué disminuyendo su anchura Δx hasta hacerla igual a cero para fines prácticos, podemos definir a la función no por sí sola sino dentro de una integral, una integral que podemos especificar que sea llevada a cabo desde -∞ hasta +∞ a sabiendas de que el “pico” tiene que estar situado necesariamente entre los dos extremos del infinito para la coordenada que representa a la variable independiente, entre el infinito negativo y el infinito positivo. Esto nos dá la clave para tratar de darle una definición matemática completa a la función delta de Dirac δ(x) con la siguiente condición:

Sin embargo, hay muchos teóricos que consideran que, siendo la función delta de Dirac una función extraordinariamente impropia, se le debe definir por el efecto que tiene sobre otra función cuando multiplica a dicha función bajo el signo de la integral. Si la función a la que multiplica es una función cualquiera f.(x), entonces la definición de la función delta de Dirac (que es la que se usa en cálculos mecánico-cuánticos) vendría siendo la siguiente: